Kolik je potřeba lidí, aby bylo pravděpodobnějšíTedy, že pravděpodobnost je větší než 50 %., že alespoň dva jedinci budou mít narozeniny ve stejný den, než každý v jiný den?
Popis problému
Mějme skupinu 
jedinců, u nichž porovnáváme data narození. Cílem je zjistit, při jak velké populaci dochází k tomu, kdy je více pravděpodobné, že více jedinců slaví narozeniny ve stejný den. Není však důležité, zda v konkrétní populaci tento jev nastane, či nikoli. Jistě tedy existuje malá skupina, v níž více jedinců bude slavit narozeniny ve stejný den, a naopak velká skupina (maximálně 
jedinců), kteří slaví narozeniny každý v jiný den.
Předpoklady
- Rok má 365 dní.
- Neuvažujeme v populaci dvojčata.
- Očekává se rovnoměrné rozdělení data narození v průběhu roku.
- Data narození jedinců v populaci jsou nezávislými jevy.
Výpočet
Označme si 
pravděpodobnost, že alespoň dva jedinci v dané populaci mají narozeniny ve stejný den. Pro jednodušší výpočet otočme otázku: jaká je pravděpodobnost, že každý jedinec má narozeniny v jiný den? Tímto dostaneme pravděpodobnost 
, pro niž musí nutně platit: 
.
Pravděpodobnost, že ve skupině čítající dva jedince má každý narozeniny v rozdílný den, dostaneme následovně:
- První jedinec může mít narozeniny ve kterýkoli den v roce.
- Druhý jedinec může mít narozeniny ve kterýkoli den vyjma v den narozenin prvního jedince.
- Obě podmínky musejí nastat současně.
(1) 
Toto pravidlo můžeme rozšířit na vícečetnou populaci, kdy pro každého dalšího přidaného jedince platí:
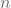-tý jedinec může mít narozeniny ve kterýkoli den vyjma v den narozenin předcházejících jedinců.
(2) 
Což můžeme zapsat i jako:
(3) 
Abychom dostali odpověď na původní otázku, stačí již pouze odečíst tuto hodnotu od jedničky, tedy:
(4) 
Přibližné hodnoty pro vybraná nalezneme v tabulce níže.
Výsledky
| Počet jedinců (N) | Pravděpodobnost (P) | Počet jedinců (N) | Pravděpodobnost (P) |
|---|---|---|---|
| 1 | 0,00 % | 21 | 44,37 % |
| 2 | 0,27 % | 22 | 47,57 % |
| 3 | 0,82 % | 23 | 50,73 % |
| 4 | 1,64 % | 24 | 53,83 % |
| 5 | 2,71 % | 25 | 56,87 % |
| 6 | 4,05 % | 26 | 59,82 % |
| 7 | 5,62 % | 27 | 62,69 % |
| 8 | 7,43 % | 28 | 65,45 % |
| 9 | 9,46 % | 29 | 68,10 % |
| 10 | 11,69 % | 30 | 70,63 % |
| 11 | 14,11 % | … | … |
| 12 | 16,70 % | 35 | 81,44 % |
| 13 | 19,44 % | 40 | 89,12 % |
| 14 | 22,31 % | 45 | 94,10 % |
| 15 | 25,29 % | 50 | 97,04 % |
| 16 | 28,36 % | 60 | 99,41 % |
| 17 | 31,50 % | 70 | 99,92 % |
| 18 | 34,69 % | 80 | 99,99 % |
| 19 | 37,91 % | 90 | 99,999 % |
| 20 | 41,14 % | 100 | 99,9999 % |
Řešení
Úvodní otázka zněla, jak velkou populaci je potřeba, aby pravděpodobnost, že alespoň dva jedinci v této populaci mají narozeniny ve stejný den, byla větší než 50 %. Z tabulky je patrné, že nejmenší , pro něž tato podmínka platí, je 
. Tedy, už ve skupině čítající 23 jedinců je větší šance, že narazíte na alespoň dva jedince, kteří mají narozeniny ve stejný den.
Poznámky
- Pamatujete si, kolik vás bylo ve třídě na základní, střední, vysoké škole?
- Ve vedlejší třídě či v kroužku, do kterého jste jako děti chodili?
- V současném zaměstnání, či restauraci, kam chodíte na obědy?
Slavila někdy nějaká dvojiceTrojice, čtveřice, … – obecně 
-tice narozeniny ve stejný den? Vsadil bych se, že alespoň jednou ANO. 🙂
Abychom neřešili pouze narozeniny, tento paradox má své uplatnění i v kryptografii. Jedná se o tzv. narozeninový útok, kdy je pro nalezení kolize v kryptovací funkci cílem najít dvě různé vstupní hodnoty, které generují stejný výstup (hash). Nalezení první kolize se předpokládá průměrně po:
(5) 
pokusech. Po dosazení za 
(počet všech možností, které mohou nastat) dostaneme:
(6) 